
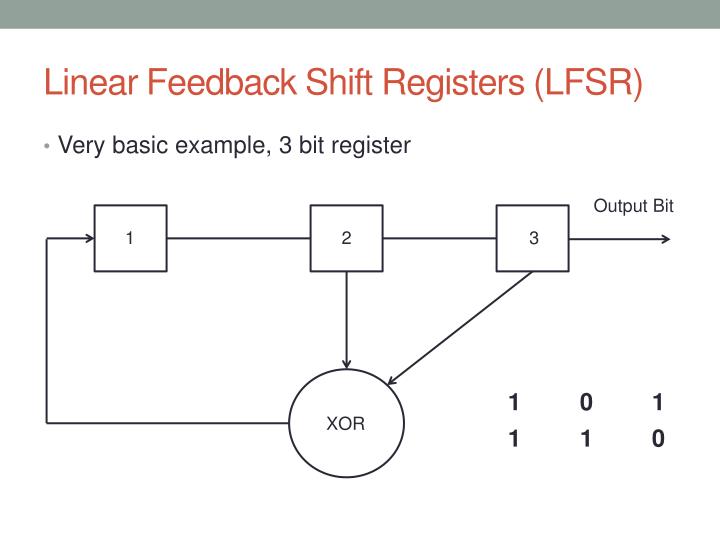
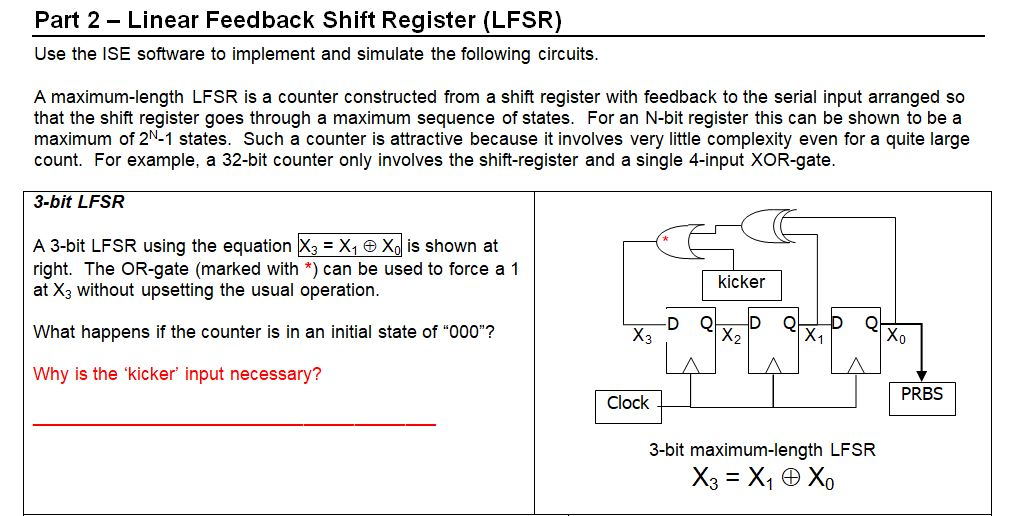
In the real world, a 4-bit CRC calculator would not be considered to provide sufficient confidence in the integrity of the transmitted data. This form of error detection is very efficient in terms of the small number of bits that have to be transmitted in addition to the data. Once all of the data bits have arrived, the receiver compares its internally generated checksum value with the checksum sent by the transmitter to determine whether any corruption occurred during the course of the transmission. The receiver contains an identical CRC calculator and generates its own checksum value from the incoming data. After all of the data bits have been transmitted, the transmitter sends its checksum value to the receiver. The final CRC value stored in the LFSR is known as a checksum, and is dependent on every bit in the data stream. Cyclic redundancy check (CRC) calculations. The stream of data bits being transmitted is used to modify the values fed back into an LFSR ( Fig 2 ).Ģ. Cyclic redundancy check (CRC) applicationsĪ traditional application for LFSRs is in cyclic redundancy check (CRC) calculations, which can be used to detect errors in data communications. gen () sage: fill = key = n = 20 sage: L = lfsr_sequence ( key, fill, 20 ) L sage: from _massey import berlekamp_massey sage: g = berlekamp_massey ( L ) g x^4 + x^3 + 1 sage: ( 1 ) / ( g. Sage: F = GF ( 2 ) l = F ( 1 ) o = F ( 0 ) sage: F = GF ( 2 ) S = LaurentSeriesRing ( F, 'x' ) x = S. OUTPUT: autocorrelation sequence of \(L\) L – a periodic sequence of elements of ZZ or GF(2) must have length \(p\) Timothy Brock (): added lfsr_autocorrelation and Timothy Brock (2005-11): added lfsr_sequence with code modified from
This is the function of the Berlekamp-Massey algorithm, implemented However, this sequence of period 15 canīe “cracked” (i.e., a procedure to reproduce \(g(x)\)) by knowing only 8 terms! The sequence of \(0,1\)’s is periodic with period \(P=2^4-1=15\) and satisfies


 0 kommentar(er)
0 kommentar(er)
